研究アウトライン
1) 研究概略
この課題研究では,干渉ブラウン運動と呼ばれる無限次元確率力学系について,干渉ポテンシャルが対数関数(2次元クーロンポテンシャル)の場合を研究する.まずDirichlet形式を用いて,確率力学系を拡散過程のレベルで構成する.更に,この拡散過程をラベル粒子系のレベルで記述する無限次元確率微分方程式を解き,確率微分方程式表現(SDE表現)を構築する.重要な例について,その時空間・相関関数の明示表現を求める.スケーリング極限を求めて,この確率力学系の大局的な構造を解明する.そのためには,確率力学系の平衡状態となる確率点場の,精密な確率幾何的考察が必要になる.この研究は,確率幾何の確率解析への応用の側面も持つ.
2) 干渉ブラウン運動とは
干渉ブラウン運動とは,ユークリッド空間Rdの中を動き回る無限個のブラウン運動粒子を表現する数学的モデルである.自由ポテンシャルをΦ,粒子間の干渉ポテンシャルをΨと表すと,干渉ブラウン運動は
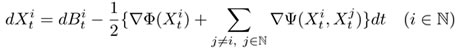
というRdN値の確率微分方程式で記述される.ここでBiは無限個の独立なd次元ブラウン運動である.
従来,無限粒子系の確率力学としてよく研究されてきたのは,格子気体である.その中でも単純排他過程は,保存的な粒子の運動を表す典型的な格子気体であり,今まで多くの研究があるが,干渉ブラウン運動は,その連続モデルに対応する.しかし連続モデル特有の難しさがあり,ランダムwalkに対するブラウン運動の役割を持つにもかかわらず,今まで十分に研究されてこなかった.更にそれら数少ないの研究は,少数の例外を除き,Ruelleクラスポテンシャルという,超安定性と遠方での可積分性を備えた干渉ポテンシャルに限られていた.このRuelleクラスポテンシャルによって構成される平衡分布は,DLR方程式をみたし,Gibbs測度と呼ばれる.このクラスは,干渉ポテンシャルの遠方での可積分性によって,遠方での漸近的独立性を持ち,様々な性質がPoisson点過程に近くなる.いわば標準的なクラスである.
本研究の特徴は,干渉ポテンシャルΨが2次元Coulombポテンシャル(対数関数)
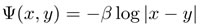
という,遠方できわめて強い影響を与えるポテンシャルの場合に,無限粒子系のレベルで干渉ブラウン運動を研究する点である.このポテンシャルに付随する平衡分布は,DLR方程式をみたさず,もはやGibbs測度とならない.実際,平衡分布の構成は,βの特別な値に対しては,ランダム行列の固有値の熱力学極限として得られていた.最近は,1次元の無限粒子系に関しては一般のβに対する平衡分布も構成されている.
干渉ブラウン運動は,Lang (1977,Z.Wahrschverw.Gebiete 39) の確率微分方程式による構成によって研究が始まった.彼は,上述のRuelle クラスのポテンシャル,つまり,超安定性という粒子が有界領域に集まり過ぎないための仮定と,正則性という無限遠方でのポテンシャルの可積分性のもとで,更に,台がコンパクトかつ滑らかなものを扱った.しかし,物理的に興味深いポテンシャルは,特異性を持つ.長田(1996 CMP176)は,特異な場合にも適用できるDirichlet形式による簡明かつ一般的な構成を行った.この結果は,Ruelleクラスであれば適用できるのみならず,Spohnの結果(1987IMA9)と組み合わせることで,Dyson干渉ブラウン運動を拡散過程のレベルで初めて構成した.更に,長田(1998PTRF112)は「2次元以上ではハードコアのブラウン球の拡散極限が常に非退化」を証明し,2次元以上の平行移動不変なGibbsの範疇(つまり干渉ポテンシャルがRuelleクラスのポテンシャル)である限り常に,干渉ブラウン運動は,拡散的スケーリングでブラウン運動とみなせるということを確立した.この結果は,当時の「2 次元以上のハードコアブラウン運動には,相転移が起こる」という予想に,否定的な解決を与
えるものである.
3) Dyson と Ginibre干渉ブラウン運動
干渉ブラウン運動において,その干渉ポテンシャルが2次元Coulombポテンシャル(対数ポテンシャル) の場合を研究するが,ここで,Dyson干渉ブラウン運動とGinibre 干渉ブラウン運動を表す確率微分方程式を記する.其々1 次元及び2 次元の平行移動不変な干渉ブラウン運動であり,最も不変性が高いという意味で,代表例である.
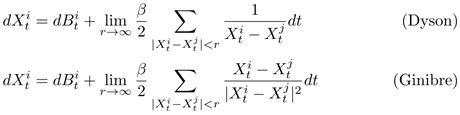
尚,この方程式の解の構成はDyson の場合はβ = 1, 2, 4,Ginibre の場合はβ = 2の場合のみ得られている.Dysonの場合は最近,平衡分布が一般のβで構成されたため,SDEの解の構成も上述の一般論から構成できるのではないかと期待されている.Ginibreについては,平衡分布の構成も一般のβに対して成されていない.